DBSCAN Clustering

-

DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

Why we need DBSCAN?

While K-Means clustering is a popular choice, it struggles with noisey data as it considers outliers as a cluster. Enters DBSCAN, an algorithm that not only detects the outliers but also removes them.


So now, let's understand, How this algorithm works?

 




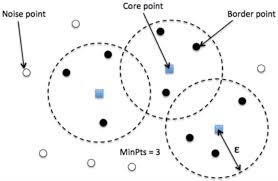
Key Ingredients of DBSCAN

  • Epsilon (ε): Think of this as the maximum distance between two points for them to be neighbors.
  • MinPts: The minimum number of points required to form a dense cluster.
  • Core Point: A point with at least MinPts neighbors within its ε-radius.
  • Border Point: Close to a core point but with fewer than MinPts neighbors.
  • Noise Point: Points that don’t fit into any cluster – the outliers.

Why Choose DBSCAN?

  • Outlier Detection: Naturally identifies noise points, making it great for spotting anomalies.
  • No Predefined Clusters: Unlike K-Means, you don’t need to specify the number of clusters beforehand.
  • Flexibility: Handles clusters of various shapes and sizes, perfect for complex datasets.

Tips for Tuning DBSCAN

Choosing the right values is key:

  • Epsilon (ε): A small eps might leave many points as noise, while a large eps could merge distinct clusters. Plot the k-distance graph to find the "elbow" point – a sweet spot for eps.
  • MinPts: Typically set to twice the number of dimensions. Adjust based on your data and domain knowledge.

Comments

Post a Comment

Popular posts from this blog

Extracting Tables and Text from Images Using Python

-
Image
In this blog, we'll explore a complete Python solution that detects and extracts tables and text from images using libraries like Transformers, OpenCV, PaddleOCR, and easyOCR. This step-by-step breakdown includes code to detect tables, extract content from individual table cells, and retrieve any remaining text in the image. Overview When working with scanned documents, such as invoices or forms, it is essential to accurately extract both structured information (like tables) and unstructured text. The approach we’ll explore uses Microsoft's pretrained object detection model to locate tables and OCR techniques to extract the text from both table cells and the rest of the image. Steps: 1. This code first detects table using microsoft's model. and save that image which contains detected table only  2. After that, from the detected table , we make a seperate image for each cell.  3. Then we read text from the image of each cell  4. Now, to read the extra texts except for the ...
Read more

Getting Started with ML

-
Image
 Types of ML :- 1) Supervised ML :- Before going for supervised learning, you need to be aware of two terminologies: Suppose, you have the data of student's age and weight. Now, for new student, just by knowing age, you want to predict his weight. So, in this case i. Dependent Variable : Age ii. Independent Variable : Weight Regression : It is applied on Numeric Data such as temperature, weight etc. Classification : It is applied on Categorial Data. There are 2 types of classification: 1.Binary Classification - Yes/No, Spam/Not Spam, etc. 2. Multiclass Classification - Small/Medium/Large, Bad/Average/Good/Excellent etc. 2) Unsupervised ML :- i. Clustering : If we have some data where there is no dependent/independent variable, then we can use clustering. suppose, we have data for salary and age. There is no relation between salary and age. So, clustering groups the data and keep the data with same characteristics together. ii. Dimensionality Reduction : Suppose, we have 100...
Read more

Linear Regression

-
Image
 Linear Regression shows the Linear Relationship between dependent features(Y-axis) and independent features(X-axis).  There are 2 types of Linear Regression: 1. Simple Linear Regression -  It has only one independent variable. Hypothesis Function for Simple Linear Regression : where: Y is the dependent variable X is the independent variable  β0 is the intercept ( the value where the regression line crosses the y-axis) β1 is the slope/weight ex : calculate weight based on age. In above figure Red dots represent Actual Data Points and black dots represent predicted values. error is calculated by (Actual Value - Predicted Value) 2. Multiple Linear Regression -  It has more than one independent features.  Hypothesis Function for Simple Linear Regression : y= a0 + a1x1 + a2x2 + a3x3 + ..  Let's understand this by example, we all know that if the size of the house is bigger, then the price also increases. But along with this, there are many other factors ...
Read more